正弦函數單調遞增區間
正弦函數 \( y = \sin(x) \) 是周期函數,其基本周期為 \( 2\pi \)。正弦函數的單調遞增區間可以通過分析其導數來確定。正弦函數的導數為 \( y' = \cos(x) \)。
當 \( \cos(x) > 0 \) 時,正弦函數是單調遞增的。由于余弦函數在 \( 2k\pi \) 到 \( (2k+1)\pi \) 之間是正的(其中 \( k \) 是整數),我們可以得出正弦函數的單調遞增區間為:
\[ 2k\pi - \frac{\pi}{2} \leq x \leq 2k\pi + \frac{\pi}{2} \]
對于 \( k = 0 \),我們得到正弦函數的一個單調遞增區間:
\[ -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \]
這個區間以 \( 2\pi \) 為周期重復出現。所以,對于任意整數 \( k \),正弦函數的單調遞增區間可以表示為:
\[ 2k\pi - \frac{\pi}{2} \leq x \leq 2k\pi + \frac{\pi}{2} \]
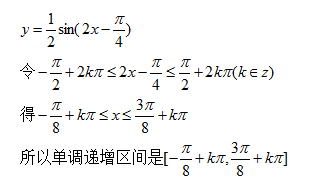
sin tan cos單調性
正弦函數 \( \sin(x) \)、余弦函數 \( \cos(x) \) 和正切函數 \( \tan(x) \) 是三角函數中的基本函數,它們在不同的區間上有不同的單調性。
1. 正弦函數 \( \sin(x) \):
- 在區間 \( [2k\pi - \frac{\pi}{2}, 2k\pi + \frac{\pi}{2}] \)(\( k \) 是整數)上單調遞增。
- 在區間 \( [2k\pi + \frac{\pi}{2}, 2k\pi + \frac{3\pi}{2}] \) 上單調遞減。
2. 余弦函數 \( \cos(x) \):
- 在區間 \( [2k\pi - \pi, 2k\pi] \) 上單調遞增。
- 在區間 \( [2k\pi, 2k\pi + 2\pi] \) 上單調遞減。
3. 正切函數 \( \tan(x) \):
- 在區間 \( (-\frac{\pi}{2} + k\pi, \frac{\pi}{2} + k\pi) \) 上單調遞增,其中 \( k \) 是整數,但不包括 \( \pm \frac{\pi}{2} \) 點,因為正切函數在這些點上無定義(垂直漸近線)。
正弦和余弦函數在每個周期內都會有單調遞增和遞減的區間,而正切函數在每個周期內除了垂直漸近線外,都是單調遞增的。需要注意的是,正切函數在每個周期的 \( \pm \frac{\pi}{2} \) 處都有間斷點。
sin和cos的遞增遞減區間
正弦函數 \( \sin(x) \) 和余弦函數 \( \cos(x) \) 是周期函數,它們在不同的區間上表現出遞增或遞減的特性。下面是它們的基本遞增和遞減區間:
正弦函數 \( \sin(x) \) 的遞增和遞減區間:
- 遞增區間:\( [2k\pi - \frac{\pi}{2}, 2k\pi + \frac{\pi}{2}] \) 對于任意整數 \( k \)。
- 遞減區間:\( [2k\pi + \frac{\pi}{2}, 2k\pi + \frac{3\pi}{2}] \) 對于任意整數 \( k \)。
余弦函數 \( \cos(x) \) 的遞增和遞減區間:
- 遞增區間:\( [2k\pi + \pi, 2k\pi + 2\pi] \) 對于任意整數 \( k \)。
- 遞減區間:\( [2k\pi, 2k\pi + \pi] \) 對于任意整數 \( k \)。
這些區間是正弦和余弦函數的基本周期的一部分,它們的周期都是 \( 2\pi \)。在這些區間內,函數值會從最小值或最大值變化到另一個極值。例如,正弦函數在 \( [2k\pi - \frac{\pi}{2}, 2k\pi + \frac{\pi}{2}] \) 區間內從 -1 增加到 1,而余弦函數在 \( [2k\pi, 2k\pi + \pi] \) 區間內從 1 減少到 -1。

 微信掃一掃打賞
微信掃一掃打賞