cos平方x求導
函數 \( \cos^2(x) \) 的導數可以通過鏈式法則和基本的三角函數導數規則來求得。
設 \( u = \cos(x) \),那么 \( \cos^2(x) = u^2 \)。
對 \( u^2 \) 求導,得到 \( \fracmqhv6cqtvbgv{dx}(u^2) = 2u \cdot \frac{du}{dx} \)。
接下來,我們需要求 \( \cos(x) \) 的導數 \( \frac{du}{dx} \)。\( \fracmqhv6cqtvbgv{dx}(\cos(x)) = -\sin(x) \)。
將 \( \cos(x) \) 的導數代入上面的表達式,我們得到:
\[ \fracmqhv6cqtvbgv{dx}(\cos^2(x)) = 2 \cdot \cos(x) \cdot (-\sin(x)) = -2 \cos(x) \sin(x) \]
我們可以將 \( -2 \cos(x) \sin(x) \) 寫成一個更簡潔的形式,使用二倍角公式 \( \sin(2x) = 2 \sin(x) \cos(x) \),得到:
\[ \fracmqhv6cqtvbgv{dx}(\cos^2(x)) = -\sin(2x) \]
所以,\( \cos^2(x) \) 的導數是 \( -\sin(2x) \)。
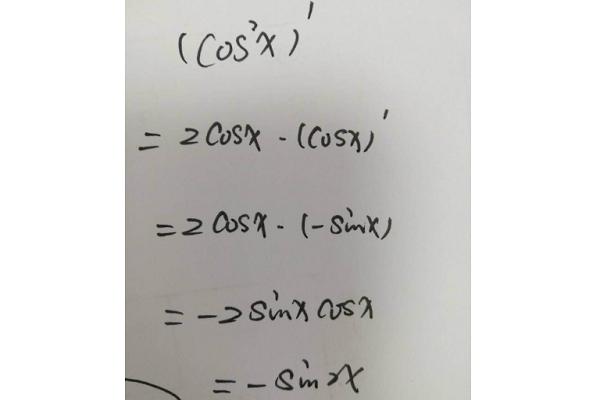
復合函數cos2X求導
復合函數 \(\cos^2(x)\) 可以通過鏈式法則求導。設 \(u = \cos(x)\),那么原函數可以寫作 \(u^2\)。
對 \(u^2\) 求導,我們得到:
\[ \fracmqhv6cqtvbgv{du}(u^2) = 2u \]
接下來,我們需要對 \(u = \cos(x)\) 求導:
\[ \frac{du}{dx} = -\sin(x) \]
應用鏈式法則,將兩個導數相乘,得到 \(\cos^2(x)\) 的導數:
\[ \fracmqhv6cqtvbgv{dx}[\cos^2(x)] = \fracmqhv6cqtvbgv{du}(u^2) \cdot \frac{du}{dx} = 2u \cdot (-\sin(x)) = -2\cos(x)\sin(x) \]
使用三角恒等式 \(\sin(2x) = 2\sin(x)\cos(x)\),可以將導數簡化為:
\[ \fracmqhv6cqtvbgv{dx}[\cos^2(x)] = -\sin(2x) \]
所以,\(\cos^2(x)\) 的導數是 \(-\sin(2x)\)。
COS2X的導數公式
函數 \(\cos^2(x)\) 的導數可以通過鏈式法則和基本的三角函數導數來計算。
設 \( u = \cos(x) \),那么 \(\cos^2(x) = u^2\)。
對 \( u^2 \) 求導,得到 \(\fracmqhv6cqtvbgv{du}(u^2) = 2u\)。
接下來,我們需要對 \( u = \cos(x) \) 求導,得到 \(\frac{du}{dx} = -\sin(x)\)。
應用鏈式法則,我們有:
\[
\fracmqhv6cqtvbgv{dx}(\cos^2(x)) = \fracmqhv6cqtvbgv{du}(u^2) \cdot \frac{du}{dx} = 2u \cdot (-\sin(x)) = -2\cos(x)\sin(x)
\]
但是,我們通常使用倍角公式來簡化這個表達式。我們知道 \(\sin(2x) = 2\sin(x)\cos(x)\),所以:
\[
-2\cos(x)\sin(x) = -\frac{1}{2}\sin(2x)
\]
\(\cos^2(x)\) 的導數是:
\[
\fracmqhv6cqtvbgv{dx}(\cos^2(x)) = -\frac{1}{2}\sin(2x)
\]

 微信掃一掃打賞
微信掃一掃打賞