整數集包括0嗎
在數學中,整數集通常包括所有的整數,即正整數、負整數和零。所以,整數集是包括0的。整數集通常用符號 \(\mathbb{Z}\) 表示。
數學中N Z Q R C代表什么
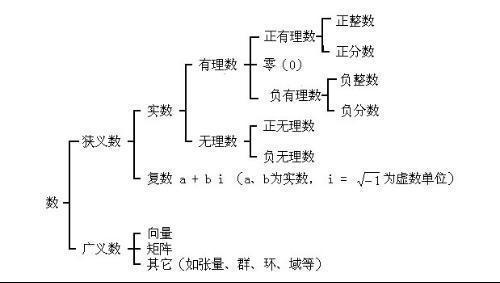
在數學中,N、Z、Q、R、C 通常代表以下集合:
1. N - 自然數集合,包括所有的正整數(1, 2, 3, ...)以及0。在一些定義中,自然數集合不包括0。
2. Z - 整數集合,包括所有的正整數、負整數以及0。
3. Q - 有理數集合,包括所有的可以表示為兩個整數比的數,即分數形式 \( \frac{p}{q} \),其中 \( p \) 和 \( q \) 是整數,且 \( q \neq 0 \)。
4. R - 實數集合,包括所有的有理數和無理數。實數可以是有限小數或無限不循環小數,它們在數軸上都有對應的點。
5. C - 復數集合,包括所有的實數和虛數。復數可以表示為 \( a + bi \) 的形式,其中 \( a \) 和 \( b \) 是實數,\( i \) 是虛數單位,滿足 \( i^2 = -1 \)。
這些集合是數學分析和代數中的基礎概念,它們定義了數的不同類型和性質。
自然數集包括0嗎
自然數集的定義在不同的數學體系中有所不同。在某些定義中,自然數集包括0,而在另一些定義中則不包括。在包括0的定義中,自然數集通常表示為 \( \mathbb{N}_0 \) 或 \( \mathbb{N} \)(取決于是否包括0),并包含所有正整數和0。而在不包括0的定義中,自然數集僅包含正整數,通常表示為 \( \mathbb{N} \)。
在現代數學中,包括0的自然數集 \( \mathbb{N}_0 \) 被廣泛接受,因為它簡化了某些數學理論,例如在數論和集合論中的應用。在討論具體的數學問題時,最好根據上下文或參考特定的數學文獻來確定自然數集是否包括0。

 微信掃一掃打賞
微信掃一掃打賞