拐點是什么意思
拐點(Inflection Point)在數學中指的是函數圖像上凹凸性發生變化的點。具體來說,如果一個函數在某點的二階導數從正變為負,或者從負變為正,那么這個點就是函數的拐點。
在經濟學和商業分析中,拐點通常用來描述一個趨勢或過程的轉折點,即從增長轉為下降,或者從下降轉為增長的點。例如,一個公司的銷售增長可能會在某個時間點達到一個拐點,之后增長速度開始放緩。
在更廣泛的語境中,拐點也可以指任何類型的轉折點或關鍵變化時刻。
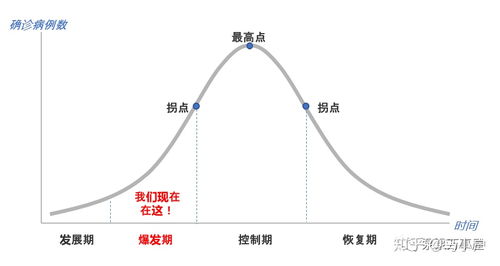
拐點是二階導數為零的點嗎
拐點不一定是二階導數為零的點,但二階導數為零的點可能是拐點。
在數學中,拐點是函數圖像上凹凸性發生變化的點。對于一個二次可微的函數 \( f(x) \),如果在某點 \( x_0 \) 處,二階導數 \( f''(x_0) \) 存在且不為零,那么這個點不一定是拐點。拐點的確切定義是:如果 \( f''(x_0) \) 存在,并且 \( x_0 \) 兩側的二階導數符號不同,即
\[ \lim_{x \to x_0^-} f''(x) \cdot \lim_{x \to x_0^+} f''(x) < 0 \]
那么 \( x_0 \) 就是函數 \( f(x) \) 的一個拐點。
如果 \( f''(x_0) = 0 \),這并不意味著 \( x_0 \) 一定是拐點。為了確定 \( x_0 \) 是否是拐點,我們還需要檢查 \( f''(x) \) 在 \( x_0 \) 附近的符號變化。如果 \( f''(x) \) 在 \( x_0 \) 附近符號不變,那么 \( x_0 \) 就不是拐點。
總結來說,拐點是二階導數改變符號的點,而二階導數為零的點可能是拐點,但需要進一步檢查二階導數在該點附近的行為。
二階導數等于0一定是拐點嗎
二階導數等于0的點不一定是拐點。拐點是指函數圖像上凹凸性發生變化的點。要確定一個點是否為拐點,我們需要檢查該點兩側的二階導數的符號是否發生變化。
1. 如果在某個點 \( x = c \) 處,二階導數 \( f''(c) = 0 \),并且 \( f''(x) \) 在 \( x = c \) 兩側的符號不同(即從正變負或從負變正),那么 \( x = c \) 是一個拐點。
2. 如果在某個點 \( x = c \) 處,二階導數 \( f''(c) = 0 \),并且 \( f''(x) \) 在 \( x = c \) 兩側的符號相同,那么 \( x = c \) 不是拐點。
如果二階導數在某個點處不存在或者該點是導數的不連續點,那么這個點也可能是拐點。
二階導數等于0只是拐點的必要條件,但不是充分條件。我們需要進一步分析二階導數在該點兩側的行為來確定是否為拐點。

 微信掃一掃打賞
微信掃一掃打賞