無理數(shù)有哪些
無理數(shù)是實數(shù)的一種,它們不能表示為兩個整數(shù)的比值,即不能寫成分數(shù)形式。無理數(shù)具有無限不循環(huán)的小數(shù)形式。以下是一些常見的無理數(shù)的例子:
1. 圓周率 \( \pi \):大約等于3.14159,是圓的周長與直徑的比值。
2. 自然對數(shù)的底數(shù) \( e \):大約等于2.71828,是自然對數(shù)的底數(shù)。
3. 黃金分割比 \( \phi \):大約等于1.61803,是相鄰斐波那契數(shù)的比值的極限。
4. 平方根:大多數(shù)數(shù)的平方根是無理數(shù),例如 \( \sqrt{2} \),\( \sqrt{3} \),\( \sqrt{5} \) 等。
5. 某些三角函數(shù)值:例如 \( \sin(1) \),\( \cos(1) \)(這里的1是以弧度為單位的角度)。
6. 某些常數(shù):如歐拉-馬斯刻若尼常數(shù) \( \gamma \),大約等于0.57721。
7. 某些特殊數(shù)列的極限:例如,當 \( n \) 趨向于無窮大時,\( (1 + \frac{1}{n})^n \) 的極限是 \( e \)。
8. 某些代數(shù)方程的根:不是所有代數(shù)方程的根都是有理數(shù),例如,多項式方程 \( x^5 - x + 1 = 0 \) 的根都是無理數(shù)。
無理數(shù)在數(shù)學和科學中非常重要,它們在幾何、物理、工程和其他領(lǐng)域都有廣泛的應用。
無理數(shù)一共有幾個
無理數(shù)是無限不循環(huán)小數(shù),它們的數(shù)量是無限的。無理數(shù)包括但不限于:
1. 圓周率 \(\pi\)
2. 自然對數(shù)的底 \(e\)
3. 黃金分割比 \(\phi\)
4. 任何非完全平方數(shù)的平方根
5. 某些三角函數(shù)值
6. 某些代數(shù)方程的根
由于無理數(shù)是無限多的,所以無法給出一個確切的數(shù)字來表示無理數(shù)的總數(shù)。
無理數(shù)有哪三類
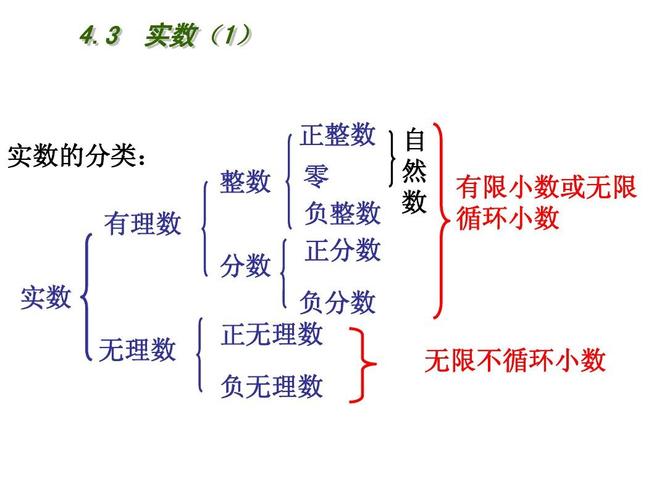
無理數(shù)是指不能表示為兩個整數(shù)的比值的實數(shù),即無限不循環(huán)的小數(shù)。無理數(shù)可以大致分為以下三類:
1. 開方開不盡的數(shù):這類無理數(shù)通常出現(xiàn)在平方根、立方根等的計算中,例如 \(\sqrt{2}\)、\(\sqrt{3}\)、\(\sqrt{2}\) 等。
2. 特定常數(shù):一些數(shù)學常數(shù)是無理數(shù),比如圓周率 \(\pi\) 和自然對數(shù)的底數(shù) \(e\)。
3. 代數(shù)無理數(shù):這類無理數(shù)不能通過有限次的加、減、乘、除和開方運算從有理數(shù)中得到。它們通常是一些代數(shù)方程(多項式方程)的解,這些方程的系數(shù)是有理數(shù),但解是無理數(shù)。例如,方程 \(x^2 - 2 = 0\) 的解 \(x = \sqrt{2}\) 就是一個代數(shù)無理數(shù)。
還有一些無理數(shù)是超越數(shù),它們既不是代數(shù)無理數(shù)也不是任何有理系數(shù)多項式的根,比如 \(\pi\) 和 \(e\) 也是超越數(shù)。

 微信掃一掃打賞
微信掃一掃打賞