不定積分怎么算
不定積分是微積分中的一個重要概念,它表示一個函數的原函數集合。求一個函數的不定積分,就是找到這個函數的所有原函數。原函數是指函數的導數等于給定函數的函數。對于一個給定的函數 \(f(x)\),其不定積分可以表示為:
\[
\int f(x) dx
\]
這表示對 \(f(x)\) 關于 \(x\) 的積分。不定積分的結果通常是一個函數加上一個常數 \(C\),因為當對一個函數求導后,結果會丟失一個常數項。所以,不定積分的一般形式是:
\[
\int f(x) dx = F(x) + C
\]
其中 \(F(x)\) 是 \(f(x)\) 的一個原函數,\(C\) 是積分常數。
求不定積分的方法有很多,以下是一些基本的方法:
1. 直接積分法:對于一些基本函數,如多項式、指數函數、對數函數等,我們可以直接根據已知的積分表來求積分。
2. 換元積分法:當積分表達式復雜時,可以通過換元法將其轉化為更簡單的形式。常見的換元法有三角換元法和代數換元法。
3. 分部積分法:當積分形式為兩個函數乘積的形式,即 \(f(x)g(x)\),可以使用分部積分法。分部積分的公式為:
\[
\int f(x)g(x) dx = f(x) \int g(x) dx - \int \left[ f'(x) \int g(x) dx \right] dx
\]
4. 有理函數積分:對于有理函數(即分子和分母都是多項式的函數),可以使用部分分式分解的方法將其分解為更簡單的部分,然后分別積分。
5. 定積分的性質:不定積分也遵循一些基本的線性性質,如加法性質和標量乘法性質。
6. 特殊技巧:對于特定類型的積分,可能需要一些特殊的技巧或公式。
在實際計算中,通常需要結合以上方法,根據具體的函數形式選擇合適的積分策略。如果你有具體的函數需要求不定積分,可以提供函數表達式,我可以幫你進一步解釋如何求解。
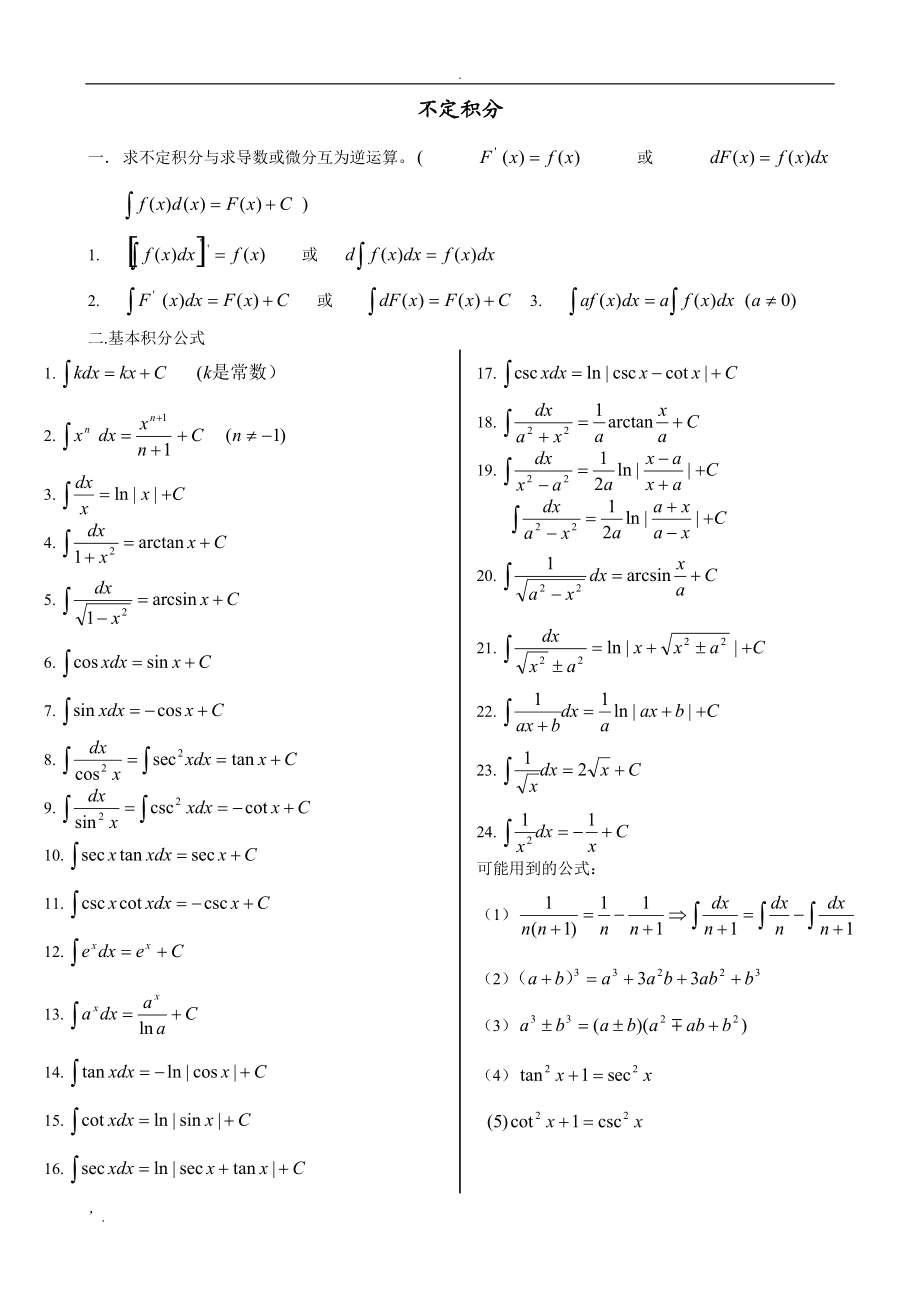
求不定積分的四種方法
不定積分是微積分中的一個重要概念,它表示求一個函數的原函數。原函數是導數的逆運算,即如果一個函數\( f(x) \)的導數是\( F'(x) \),那么\( F(x) \)就是\( f(x) \)的一個原函數。在求解不定積分時,有幾種常用的方法,下面我將介紹四種基本的方法:
1. 直接積分法:
這種方法適用于一些簡單的函數,可以直接通過已知的導數公式來找到原函數。例如,對于多項式函數,指數函數,三角函數等,我們可以直接應用基本的積分公式來求解。
2. 換元積分法:
當一個積分表達式看起來復雜,但是可以通過代換變量簡化時,可以使用換元積分法。這種方法包括兩種主要的形式:
- 第一類換元法:也稱為湊微分法,主要用于積分中含有根式的情況,通過代換將根式轉化為更簡單的形式。
- 第二類換元法:用于積分中含有特定形式的多項式或三角函數的情況,通過代換將積分表達式轉化為更易于處理的形式。
3. 分部積分法:
分部積分法是一種用于求解積分形式為\( \int u dv \)的技巧,其中\( u \)和\( dv \)是已知的函數。分部積分的公式為:
\[
\int u dv = uv - \int v du
\]
選擇適當的\( u \)和\( dv \)是應用分部積分法的關鍵。
4. 有理函數積分法:
當積分函數是一個有理函數(即分子和分母都是多項式的函數)時,可以使用有理函數積分法。這種方法通常涉及將有理函數分解為更簡單的部分,然后分別對這些部分進行積分。
這些方法在解決不同類型的積分問題時各有優勢,實際應用時可能需要結合使用。在求解不定積分時,通常還需要加上一個常數C,因為不定積分表示的是一族函數,而不是單個函數。
不定積分(公式大全)
不定積分是微積分學中的一個重要概念,它與導數相對應,用于求解函數的原函數。以下是一些常見的不定積分公式,這些公式在解決不定積分問題時非常有用:
1. \(\int a \cdot f(x) dx = a \cdot \int f(x) dx\),其中 \(a\) 是常數。
2. \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\),其中 \(n \neq -1\)。
3. \(\int \frac{1}{x} dx = \ln|x| + C\)。
4. \(\int e^x dx = e^x + C\)。
5. \(\int a^x dx = \frac{a^x}{\ln a} + C\)。
6. \(\int \sin x dx = -\cos x + C\)。
7. \(\int \cos x dx = \sin x + C\)。
8. \(\int \sec^2 x dx = \tan x + C\)。
9. \(\int \csc^2 x dx = -\cot x + C\)。
10. \(\int \sec x \tan x dx = \sec x + C\)。
11. \(\int \csc x \cot x dx = -\csc x + C\)。
12. \(\int \frac{1}{a^2 - x^2} dx = \frac{1}{2a} \ln \left| \frac{x-a}{x+a} \right| + C\)。
13. \(\int \frac{1}{1 + x^2} dx = \arctan x + C\)。
14. \(\int \frac{1}{\sqrt{1 + x^2}} dx = \sinh^{-1} x + C\) 或 \(\cosh^{-1} x + C\)。
15. 部分分式積分:對于形如 \(\frac{p(x)}{q(x)}\) 的有理函數,其中 \(p(x)\) 和 \(q(x)\) 是多項式,且 \(q(x)\) 的次數高于 \(p(x)\),可以使用部分分式展開來簡化積分。
16. 三角換元積分:對于某些含有 \(a^2 - x^2\) 或 \(a^2 + x^2\) 的積分,可以使用三角換元來簡化計算。
17. 有理函數積分:對于有理函數 \(\frac{p(x)}{q(x)}\) 的積分,可以通過多項式的長除法和部分分式展開來求解。
18. 定積分的性質:不定積分具有線性性質,即 \(\int (f(x) + g(x)) dx = \int f(x) dx + \int g(x) dx\)。
19. 換元積分法:對于某些復雜的積分,可以通過合適的變量替換來簡化積分表達式。
20. 分部積分法:對于形如 \(\int u dv\) 的積分,可以使用分部積分公式 \(\int u dv = uv - \int v du\) 來求解。
這些是一些基本的不定積分公式,實際應用中可能需要結合具體的積分問題來選擇合適的方法。在求解不定積分時,通常需要加上一個常數 \(C\) 來表示任意常數項,因為原函數是唯一的確定的函數加上一個常數項。

 微信掃一掃打賞
微信掃一掃打賞